Kinh Nghiệm về How many on to functions are there from a set with six elements to a set with three elements? 2022
Bùi Nam Khánh đang tìm kiếm từ khóa How many on to functions are there from a set with six elements to a set with three elements? được Cập Nhật vào lúc : 2022-09-28 11:36:23 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.In this article, we are discussing how to find number of functions from one set to another. For understanding the basics of functions, you can refer this: Classes (Injective, surjective, Bijective) of Functions.
Nội dung chính- How many onto functions are there from a set with 6 elements to a set with 4 elements?How many total functions are there from a set with three elements to a set with four elements?How many functions are there from a set with 3 elements to a set with 5 elements?How many functions are there from a set with two elements to a set with three elements?
Number of functions from one set to another: Let X and Y are two sets having m and n elements respectively. In a function from X
to Y, every element of X must be mapped to an element of Y. Therefore, each element of X has ‘n’ elements to be chosen from. Therefore, total number of functions will be n×n×n.. m times = nm.
For example: X = a, b, c and Y = 4, 5. A function from X to Y can be represented in Figure 1.
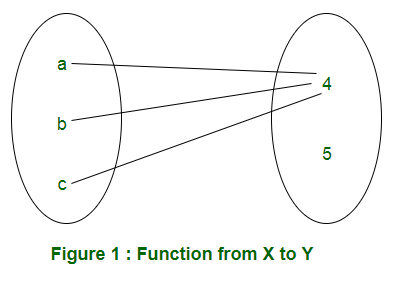
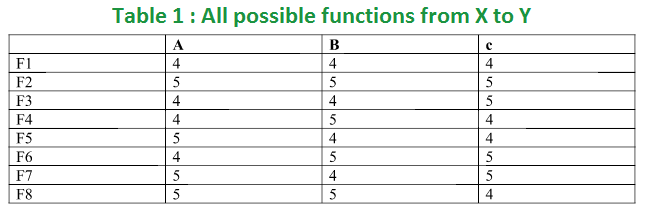
Considering all possibilities of mapping elements of X to elements of Y, the set of functions can be represented in Table 1.
Examples: Let us discuss gate questions based on this:
- Q1. Let X, Y, Z be sets of sizes x, y and z respectively. Let W = X x Y. Let E be the set of all subsets of W. The number of functions from Z to E is:
(A) z2xy
(B) z x 2xy
(C) z2x + y
(D) 2xyz
Solution: As W = X x Y is given, number of elements in W is xy. As E is the set of all subsets of W, number of elements in E is 2xy. The number of functions from Z (set of z elements) to E (set of 2xy elements) is 2xyz. So the correct option is (D)
(A) 12
(B) 13
(C) 15
(D) 16
Solution: As given in the question, S denotes the set of all functions f: 0, 14 → 0, 1. The number of functions from 0,14 (16 elements) to 0, 1 (2 elements) are 216. Therefore, S has 216 elements. Also, given, N denotes the number of function from S(216 elements) to 0, 1(2 elements). Therefore, N has 2216 elements. Calculating required value,
Log2(Log2 (2216)) =Log216 = 16
Therefore, correct option is (D).
Number of onto functions from one set to another – In onto function from X to Y, all the elements of Y must be used. In the example of functions from X = a, b, c to Y = 4, 5, F1 and F2 given in Table 1 are not onto. In F1, element 5 of set Y is unused and element 4
is unused in function F2. So, total numbers of onto functions from X to Y are 6 (F3 to F8).
- If X has m elements and Y has 2 elements, the number of onto functions will be 2m-2.
Explanation: From a set of m elements to a set of 2 elements, the total number of functions is 2m. Out of these functions, 2 functions are not onto (If all elements are mapped to 1st element of Y or all elements are mapped to 2nd element of Y). So, number of onto functions is 2m-2.
If X has m elements and Y has n elements, the number if onto functions are,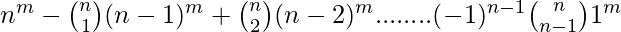
Important notes
–
- The formula works only if m ≥ n.If m < n, the number of onto functions is 0 as it is not possible to use all elements of Y.
Q3. The number of onto functions (surjective functions) from set X = 1, 2, 3, 4 to set Y = a, b, c is:
(A) 36
(B) 64
(C) 81
(D) 72
Solution: Using m = 4 and n = 3, the number of onto functions is:
34 – 3C1(2)4
+ 3C214 = 36.
$begingroup$
Consider functions from a set with $5$ elements to a set with $3$ elements.
(a) How many functions are there?
(b) How many are one-to-one?
(c) How many are onto?
a) Each element mapped to $3$ images.
$3 cdot 3 cdot 3 cdot 3 cdot 3$
b) $0$
c) How do I do this?
Edit: I tried doing this way.
EDIT: There can be a set of cardinality 3,1,1 or 2,2,1.
For 3,1,1: 5C3 * 2C1 * 1C1 * 3!
For 2,2,1: 5C2 * 3C2 * 1C1 * 3!
And i realized my 3! is wrong. Should be * 3 only. Why is that so?
asked Apr 28, 2022 8:47
RStyleRStyle
6071 gold badge5 silver badges14 bronze badges
$endgroup$
5
$begingroup$
You correctly found that there are $3^5$ functions from a set with five elements to a set with three elements. However, this counts functions with fewer than three elements in the range. We must exclude those functions. To do so, we can use the Inclusion-Exclusion Principle.
There are $binom31$ ways of excluding one element in the codomain from the range and $2^5$ functions from a set with five elements to the remaining two elements in the codomain.
There are $binom32$ ways of excluding two elements in the codomain from the range and $1^5$ functions from a set with five elements to the remaining element in the codomain.
By the Inclusion-Exclusion Principle, the number of surjective (onto) functions from a set with five elements to a set with three elements is
$$3^5 - binom312^5 + binom321^5$$
answered Apr 28, 2022 9:11
N. F. TaussigN. F. Taussig
68.2k13 gold badges52 silver badges70 bronze badges
$endgroup$
2
$begingroup$
Hint on c)
The "onto"-function will induce a partition of its domain (as any function) and this partition (actually the fibres of the function) will - because it is onto - have exactly $3$ elements. So to be found is in the first place how many such partitions exist. A fixed partition gives room for $3times2times1=6$ functions.
So you end up with: $$6timestextnumber of partitions on 1,2,3,4,5\text that have exactly 3text elements$$
Also have a look here (especially the counting of partitions).
A general formula for the number of onto-functions $1,dots,n\to1,dots,k$ is: $$k!S(n,k)$$where $S(n,k)$ stands for the Stirling number of the second kind.
answered Apr 28, 2022 8:55

drhabdrhab
143k9 gold badges70 silver badges191 bronze badges
$endgroup$
1
How many onto functions are there from a set with 6 elements to a set with 4 elements?
= 6 and S(4, 3) = 6. Thus, there are 36 onto functions.How many total functions are there from a set with three elements to a set with four elements?
The correct choice is C. The total number of injective mappings from the set containing 3 elements into the set containing 4 elements is 4P3 = 4! = 24.How many functions are there from a set with 3 elements to a set with 5 elements?
1 Answer. Image of each element of A can be taken in 3 ways. ∴ Number of functions from A to B = 35 = 243.How many functions are there from a set with two elements to a set with three elements?
Thus there are 32 32 32 possible functions. Tải thêm tài liệu liên quan đến nội dung bài viết How many on to functions are there from a set with six elements to a set with three elements?
