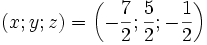Kinh Nghiệm Hướng dẫn Hệ phương trình nào sau đây là hệ phương trình số 1 3 ẩn 2022
Bùi Khánh Ngọc đang tìm kiếm từ khóa Hệ phương trình nào sau đây là hệ phương trình số 1 3 ẩn được Cập Nhật vào lúc : 2022-03-27 23:07:11 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
07/09/2022 579
A. 3x−22y=72x+33y=−26
Đáp án đúng chuẩn
Nội dung chính- A. 3x−22y=72x+33y=−26CÂU HỎI HOT CÙNG CHỦ ĐỀA. Hệ phương trình vô nghiệmB. Hệ phương trình có nghiệm duy nhấtC. Hệ phương trình có vô số nghiệmD. Hệ phương trình có nhiều hơn nữa một nghiệmVideo liên quan
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Tìm tất cả những giá trị của m để hệ phương trình sau vô nghiệm
mx+y=3x+my=2
Xem đáp án » 07/09/2022 1,423
Cho hệ phương trình. Tìm m để hệ phương trình (I) tương đương với hệ phương trình
Xem đáp án » 07/09/2022 560
Cho những hệ phương trình sau:
4x+3y=72x+5y=−7 I; 4x−3y=212x−5y=21 II; −5c−3y=−112x+9y=−19 III
Hai hệ phương trình nào tương đương với nhau?
Xem đáp án » 07/09/2022 401
Tìm tất cả những giá trị của a để hệ phương trình sau có một nghiệm duy nhất:
Xem đáp án » 07/09/2022 398
Cho hệ phương trình x2+y2=82x2−3y2=1
Hệ có số nghiệm là:
Xem đáp án » 07/09/2022 206
Các đường thẳng 2x + 3y = 20; 3x – 5y = 11 và x + y = 9 có đồng quy tại một điểm không?
Xem đáp án » 07/09/2022 144
Nghiệm của hệ phương trình 2x−3y=12x+2y=−2 là:
Xem đáp án » 07/09/2022 122
Cho hệ phương trình 3x+2y=−2x+2y=6 I
Tìm m để hệ phương trình (I) tương đương với hệ phương trình x+y=12x−y=m II
Xem đáp án » 07/09/2022 75
Xác định a để hai hệ phương trình sau tương đương
x−y=12x+y=2 I ax−2y=2x+ay=1 II
Xem đáp án » 07/09/2022 59
Tìm giá trị của m để ba đường thẳng sau đồng quy
(d1): 5x + 11y = 8,
(d2): 10x – 7y = 74,
(d3): 4mx + (2m – 1)y = m + 2
Xem đáp án » 07/09/2022 59
Cặp số (−13; −5) là nghiệm của hệ phương trình nào sau đây?
Xem đáp án » 07/09/2022 54
Giải hệ phương trình X+Y=82X−3Y=1
Đáp số: (X; Y) = (…; …)
Xem đáp án » 07/09/2022 49
Cho hệ phương trình mx+y=14x+my=2. Giải hệ phương trình khi m = 1
Xem đáp án » 07/09/2022 48
Tìm hai số a và b sao cho 5a – 4b = −5 và đường thẳng ax + by = −1 đi qua điểm A(−7; 4)
Xem đáp án » 07/09/2022 47
Cho hệ phương trình 3x−y=−m3x−m2y=−3. Giải hệ phương trình với m = 0
Xem đáp án » 07/09/2022 36
03/09/2022 179
A. Hệ phương trình vô nghiệm
B. Hệ phương trình có nghiệm duy nhất
Đáp án đúng chuẩn
C. Hệ phương trình có vô số nghiệm
D. Hệ phương trình có nhiều hơn nữa một nghiệm
Câu hỏi trên thuộc đề trắc nghiệm
Trắc nghiệm Toán 10 Chương 3 Bài 3Lớp 10 Toán học Lớp 10 - Toán học
Phương trình số 1 ba ẩn có dạng tổng quát là
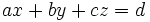 trong đó x, y, z là ba ẩn; a, b, c, d là những thông số và a, b, c không đồng thời bằng 0.
trong đó x, y, z là ba ẩn; a, b, c, d là những thông số và a, b, c không đồng thời bằng 0.
Hệ ba phương trình số 1 ba ẩn có dạng tổng quát là:
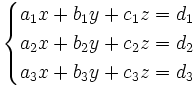 trong đó x, y, z là ẩn; những chữ còn sót lại là những thông số.
trong đó x, y, z là ẩn; những chữ còn sót lại là những thông số.
Mỗi bộ ba số (x0;y0;z0) là nghiệm đúng cả ba phương trình của hệ được gọi là một nghiệm của hệ phương trình . Chẳng hạn, 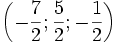 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
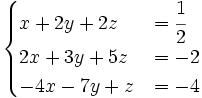 Dạng đặc biệt: Hệ phương trình (2):
Dạng đặc biệt: Hệ phương trình (2):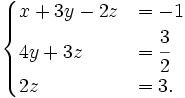 Hệ này còn có nghiệm là
Hệ này còn có nghiệm là 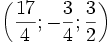 .Hệ phương trình (2) trên có dạng đặc biệt: Phương trình trên cùng có đủ ba ẩn; phương trình thức hai có hai ẩn y và z, khuyết ẩn x; phương trình ba có một ẩn z, khuyết ẩn x và ẩn y. Người ta thường gọi là hệ phương trình dạng tam giác.
.Hệ phương trình (2) trên có dạng đặc biệt: Phương trình trên cùng có đủ ba ẩn; phương trình thức hai có hai ẩn y và z, khuyết ẩn x; phương trình ba có một ẩn z, khuyết ẩn x và ẩn y. Người ta thường gọi là hệ phương trình dạng tam giác.
Việc giải hệ phương trình dạng tam giác này rất đơn giản. Từ phương trình cuối tính được z rồi thay vào phương trình thứ hai ta tính được y và ở đầu cuối thay z và y tính được vào phương trình đầu sẽ tính được x.
Chú ý: Mọi hệ ba phương trình số 1 ba ẩn đều biến hóa được về dạng tam giác, bằng phương pháp khử dần ẩn số(*).
Dạng 1. Giải hệ phương trìnhVí dụ 1. Giải hệ
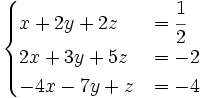
Lời giải
Nhân hai vế của phương trình thứ nhất của hệ (6) với -2 rồi cộng vào phương trình thứ hai theo từng vế tương ứng, nhân hai vế của phương trình thứ nhất với 4 rồi cộng vào phương trình thứ ba theo từng vế tương ứng, ta được hệ phương trình (đã khử x ở hai phương trình cuối)
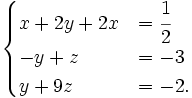 Tiếp tục cộng những vế tương ứng của phương trình thứ hai và phương trình thứ ba của hệ mới nhận được, ta được hệ phương trình tương đương dạng tam giác:
Tiếp tục cộng những vế tương ứng của phương trình thứ hai và phương trình thứ ba của hệ mới nhận được, ta được hệ phương trình tương đương dạng tam giác: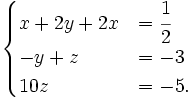 Ta thuận tiện và đơn giản giải ra được
Ta thuận tiện và đơn giản giải ra được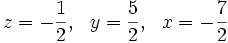
Vậy hệ có một nghiệm là:
$left{ beginalign& x+y+z=3 \& 2x-y+2z=-3 \& x-3y-3z=-5 \endalign right.$
có nghiệm là:
A. (1; 3;–1) B. (1; 3;–2) C. (1; 2; –1) D. (1; –3; –1)
Lời giải
Chọn A.
Giải tự luận:
Cách 1:
Cộng phương trình thứ nhất và thứ hai theo vế, ta được hệ phương trình sau:
$left{ beginalign& x+y+z=3 \& 3x+3z=0 \& x-3y-3z=-5 \endalign right.$
Nhân hai vế phương trình đầu với 3, xong đem cộngtheo vế với phương trình cuối, ta được hệ
$left{ beginalign& x+y+z=3 \& x+z=0 \& 4x=4 \endalign right.$
Từ phương trình cuối ta có $x=1,$ thay vào phương trình hai tính được $z=-1.$ thay đồng thời vào phương trình đầu thì $y=3.$ Vậy nghiệm của hệ là $(1;,3;,-1).$
Cách 2:Rút ẩn từ một phương trình thay vào hai phương trình còn sót lại.
Từ phương trình đầu ta rút được $z=3-x-y,$ đem thay vào hai phương trình còn sót lại ta được hệ:
[left{ beginalign& z=3-x-y \& 2x-y+2z=-3 \& x-3y-3z=-5 \endalign right.]
Thế phương trình đầu vào hai phương trình sau ta có hệ:
[left{ beginalign& z=3-x-y \& -3y=-9 \& 4x=4 \endalign right.]
Từ hai phương trình cuối dễ tính được $x=1,,y=3.$Thay vào phương trình đầu được $z=-1.$
Vậy nghiệm của hệ là $(1;,3;,-1).$
Giải trắc nghiệm:
Bấm máy tính Chọn A.
Dạng 2 : Tìm điềm kiện của tham số để hệ ba phương trình số 1 3 ẩn có nghiệm thỏa điều kiện cho trước ?
Phương pháp giải:
Hệ có dạng: [left{ beginalign& a_1x+b_1y+c_1z=d_1 \ & a_2x+b_2y+c_2z=d_2 \ & a_3x+b_3y+c_3z=d_3 \endalign right.cdot ] Một nghiệm của hệ là bộ 3 số $(x_o;y_o;z_o)$ thỏa cả 3 phương trình của hệ. Nguyên tắc chung để giải những hệ phương trình nhiều ẩn là khử bớt ẩn để đưa về những phương trình hay hệ phương trình có số ẩn ít hơn. Để khử bớt ẩn, ta cũng hoàn toàn có thể dùng những phương pháp cộng đại số, phương pháp thế như đối với hệ phương trình số 1 hai ẩn.
Ví dụ 1: Tìm tất cả những giá trị thực của tham số $m$ để hệ:
$left{ beginarray*20c x + y + left( m + 1 right)z = 2&(1)\ beginarrayl 3x + 4y + 2z = m + 1\ 2x + 3y – z = 1 endarray&beginarrayl (2)\ (3) endarray
endarray right.$
vô số nghiệm?
A.$m=2$. B.$m=-3$ C.$m=1$ D.$mne 2$
Chọn A.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ $(3)$suy ra $z=2x+3y-1$. Thế vào hai PT (1)và (2) ta được
$left{ beginarrayl x + y + (m + 1)(2x + 3y – 1) = 2\ 3x + 4y + 2(2x + 3y – 1) = m + 1
endarray right.$
$ Leftrightarrow left{ beginarrayl (2m + 3)x + (3m + 4)y = m + 3\ 7x + 10y = m + 3
endarray right.$
Ta có:
[D=left| beginmatrix 2m+3 & 3m+4 \ 7 & 10 \endmatrix right|=2-m]
[D_x=left| beginmatrix m+3 & 3m+4 \ m+3 & 10 \endmatrix right|=3(m+3)(2-m)]
[D_y=left| beginmatrix 2m+3 & m+3 \ 7 & m+3 \endmatrix right|=-2(m+3)(2-m)].
Hệ phương trình có vô số nghiệm $Leftrightarrow D=D_x=D_y=0Leftrightarrow m=2$
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt những giá trị của $m$ ở 3 đáp án A, B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án A.
Ví dụ 2: Tìm tất cả những giá trị thực của tham số $m$ để hệ:
$left{ beginarray*20c x + y – z = 1&(1)\ beginarrayl 2x + 3y + mz = 3\ x + my + 3z = 2 endarray&beginarrayl (2)\ (3) endarray
endarray right.$
vô nghiệm?
A.$m=2$. B.$m=-3$
C.$m=1$ D.$mne 2,mne -3$
Chọn B.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ (1) suy ra z=x+ y-1. Thay vào (2) và (3) ta được
$left{ beginarrayl 2x + 3y + m(x + y – 1) = 3\ x + my + 3(x + y – 1) = 2
endarray right.$
$ Leftrightarrow left{ beginarrayl (m + 2)x + (m + 3)y = m + 3\ 4x + (m + 3)y = 5
endarray right.$
Ta có:
$D = left| beginarray*20c m + 2&m + 3\ 4&m + 3
endarray right| = (m + 3)(m – 2)$
$D_x = left| beginarray*20c m + 3&m + 3\ 5&m + 3
endarray right| = (m + 3)(m – 2)$
$D_y = left| beginarray*20c m + 2&m + 3\ 4&5
endarray right| = m – 2$
Với: $rmD = 0 Leftrightarrow left[ beginarrayl m = 2\ m = – 3
endarray right.$
+ Khi $m=2$ ta có $textD=D_x=D_y=0$ nên hệ phương trình có nghiệm là nghiệm của phương trình $4x+5y=5Leftrightarrow y=frac-45x+1$.
Do đó hệ phương trình có nghiệm là $left( x;y right)=left( 5t;-4t+1 right),,,tin mathbbR$.
+ Khi $m=-3$ ta có $D=0,,D_yne 0$ nên hệ phương trình vô nghiệm
Chọn đáp án B.
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt những giá trị của $m$ ở 3 đáp án A, B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án B.
Ví dụ 3: Tìm tất cả những giá trị thực của tham số $m$ để hệ:
$left{ beginarrayl mx + y = 1\ my + z = 1\ x + mz = 1
endarray right.$
có nghiệm duy nhất?
A.$mne 1$. B.$m=1$
C.$m=-1$ D.$mne -1$
Chọn D.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ (2) suy ra z=1-my . Thay vào (3) ta được:
$left{ beginarrayl mx + y = 1\ x – m^2y = 1 – m
endarray right.$
Hệ có nghiệm duy nhất lúc:
$fracm1 ne frac1 – m^2 Leftrightarrow m ne – 1$
Chọn đáp án D.
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt những giá trị của $m$ ở 3 đáp án B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án B.
1. Giải những hệ phương trình a)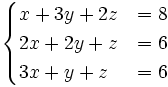 b)
b) 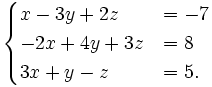
2. Một shop bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, lệch giá là 5 349 000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, lệch giá là 5 600 000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, lệch giá là 5 259 000 đồng. Hỏi giá cả mỗi áo, mỗi quần và mỗi váy là bao nhiêu?
3. Giải những hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai) a)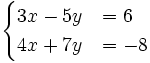 b)
b) 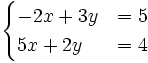 c)
c) 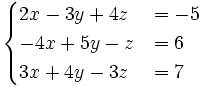 d)
d) 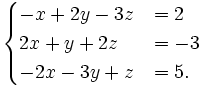
[embed]https://www.youtube.com/watch?v=bmE0JI83dIk[/embed]