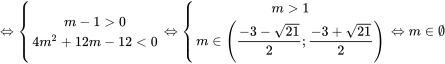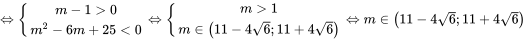Thủ Thuật về Tìm tất cả những giá trị thực của tham số m để hệ bất phương trình 3 0 1 xmx vô nghiệm Chi Tiết
Bùi Phương Thảo đang tìm kiếm từ khóa Tìm tất cả những giá trị thực của tham số m để hệ bất phương trình 3 0 1 xmx vô nghiệm được Cập Nhật vào lúc : 2022-03-27 01:13:11 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
VnHocTap.com ra mắt đến những em học viên lớp 10 nội dung bài viết Tìm giá trị của tham số để hệ bất phương trình có tập nghiệm thỏa điều kiện cho trước, nhằm mục đích giúp những em học tốt chương trình Toán 10.
Nội dung chính- Tìm tham số m để bất phương trình có nghiệm đúng với mọi x thuộc RTìm m để bất phương trình nghiệm đúng với mọi x thuộc RVideo liên quan
Nội dung nội dung bài viết Tìm giá trị của tham số để hệ bất phương trình có tập nghiệm thỏa điều kiện cho trước: Tìm giá trị của tham số để hệ bất phương trình có tập nghiệm thỏa điều kiện cho trước. BÀI TẬP DẠNG 6. Ví dụ 1. Cho hệ bất phương trình x − m + 1 > 0, m + 2 − x ≥ 0. Tìm tất cả những giá trị thực của tham số m để hệ bất phương trình. a) Nghiệm đúng với mọi x ∈ [−2; −1). b) Có duy nhất một nghiệm thuộc [1; 3). c) Có nghiệm thuộc (−1; 1). Lời giải. Ta có x − m + 1 > 0, m + 2 − x ≥ 0 ⇔ x > m − 1, x ≤ m + 2. Suy ra hệ có tập nghiệm S = (m − 1; m + 2]. a) Hệ có nghiệm đúng với mọi x ∈ [−2; −1) khi và chỉ khi [−2; −1) ⊂ S ⇔ m − 1 < −2, m + 2 ≥ −1 ⇔ −3 ≤ m 1, mx + m2 − 2m ≥ 0. Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình a) Nghiệm đúng với mọi x ∈ [−1; +∞). b) Có nghiệm thuộc [0; 3). Gọi S1, S2, S lần lượt là tập nghiệm của (1),(2) và của hệ. Khi đó S1 = (1 − m; +∞) và. Với m = 0 ta có S2 = R ⇒ S = S1 ∩ S2 = (1 − m; +∞). Với m > 0 ta có S2 = [2 − m; +∞) ⇒ S = S1 ∩ S2 = [2 − m; +∞). Với m 0 ta có [−1; +∞) ⊂ S ⇔ 2− m ≤ −1 ⇔ m ≥ 3. Kết hợp điều kiện m > 0 ta có m ≥ 3 thoả mãn. Với m < 0 ta có S = (1 − m; 2 − m] 6⊃ [−1; +∞) ⇒ m 0 ta có [0; 3) ∩ S 6= ∅ ⇔ 2 − m −1. Kết hợp điều kiện m > 0 ta có m > 0 thoả mãn. Với m < 0 ta có [0; 3) ∩ S 6= ∅ ⇔ 1 − m 0 ⇔ −2 < m < 2. Kết hợp điều kiện m < 0 ta có −2 < m 0, 6m − 2 − x ≥ 0. Tìm tất cả các giá trị thực của tham số m để hệ có nghiệm đúng với mọi x ∈ [−2; 3]. Hệ có nghiệm đúng với mọi x ∈ [−2; 3] ⇔ 1 − 2m 3. Bài 2. Cho hệ bất phương trình x + m > 2, (m − 1)x − mét vuông + 4m − 3 > 0. Tìm tất cả những giá trị thực của tham số m để hệ a) Có nghiệm thuộc (−∞; 2). b) Có nghiệm thuộc [−1; 3]. c) Nghiệm đúng với mọi x ∈ [−1; 3]. Giải và biện luận hệ ta có. Với m ≤ 1 ta có hệ vô nghiệm. Với m > 1, hệ có tập nghiệm S = (maxm − 3; 2 − m; +∞). a) Hệ có nghiệm thuộc (−∞; 2) ⇔ maxm − 3; 2 − m < 2 ⇔ m − 3 < 2, 2 − m < 2 ⇔ 0 < m 1 ta có một < m < 5 thỏa mãn. b) Hệ có nghiệm thuộc [−1; 3] ⇔ maxm − 3; 2 − m < 3 ⇔ m − 3 < 3, 2 − m < 3 ⇔ −1 < m 1 ta có một < m < 5 thỏa mãn. c) Hệ có nghiệm đúng với mọi x ∈ [−1; 3] ⇔ maxm − 3; 2 − m < −1 ⇔ m − 3 < −1, 2 − m < −1 ⇔ m 3 vô nghiệm m.
Bài 3. Cho hệ bất phương trình mx − 1 < 0, (3m − 2)x − m < 0. Tìm tất cả những giá trị thực của tham số m để hệ nghiệm đúng với mọi x dương. Với m = 0, hệ có tập nghiệm S = (0; +∞) ⇒ m = 0 thỏa mãn. Vậy có duy nhất giá trị m = 0 thỏa mãn đề bài. Bài 4. Cho hệ bất phương trình m(x − 1) + 2 ≥ 0, x − m ≤ 2. Tìm tất cả những giá trị thực của tham số m để hệ bất phương trình nghiệm đúng với mọi x thuộc [0; 1]. Với m = 0, hệ có tập nghiệm S = (−∞; 2) ⊃ [0; 1] ⇒ m = 0 thỏa mãn. Với m < 0, hệ có tập nghiệm S = (−∞; minß). Hệ nhận mọi x thuộc [0; 1] là nghiệm ⇔ m ≥ −1. Kết hợp điều kiện m < 0 ta có −1 ≤ m 0, hệ nhận mọi x ∈ [0; 1] là nghiệm ⇔ m + 2 ≥ 1 ⇔ 0 0 ta có 0 < m ≤ 2 thỏa mãn. Vậy tập những giá trị m thỏa mãn là [−1; 2].
Tìm tham số m để bất phương trình có nghiệm đúng với mọi x thuộc R
Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc R môn Toán lớp 10 vừa được VnDoc.com biên soạn và xin gửi tới bạn đọc cùng tham khảo. Bài viết tổng hợp phương pháp giải, những dạng bài tập và hướng dẫn rõ ràng về bất phương trình phổ biến trong những kì thi, bài kiểm tra trong chương trình trọng tâm Toán 10 nhằm mục đích giúp những bạn nắm vững kiến thức và kỹ năng cơ bản, nâng cao kĩ năng tư duy bài tập. Chúc những bạn ôn tập hiệu suất cao! Mời những bạn cùng tham khảo rõ ràng nội dung bài viết dưới đây nhé.
Để tiện trao đổi, chia sẻ kinh nghiệm tay nghề về giảng dạy và học tập những môn học lớp 10, VnDoc mời những thầy cô giáo, những bậc phụ huynh và những bạn học viên truy cập nhóm riêng dành riêng cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của những thầy cô và những bạn.
Tìm m để bất phương trình nghiệm đúng với mọi x thuộc R
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích mục tiêu thương mại
Phương pháp: Đối với những bài toán tìm điều kiện để bất phương trình nghiệm đúng với mọi x hay bất phương trình vô nghiệm ta sử dụng những lập luận như sau: (ta xét với bất phương trình bậc hai một ẩn)
- f(x) > 0 vô nghiệm ⇔ f(x) ≤ 0 nghiệm đúng với ∀x ∈
Ví dụ 1: Cho bất phương trình (m - 1)x2 + 2mx - 3 > 0. Tìm giá trị của m để bất phương trình nghiệm đúng với mọi x thuộc .
Hướng dẫn giải
Đặt (m - 1)x2 + 2mx - 3 = f(x)
TH1: m - 1 = 0 ⇒ m = 1. Thay m = 1 vào bất phương trình ta được: 2x - 3 > 0⇒ (Loại)
TH2: m - 1 ≠ 0 ⇔ m ≠ 1
Để bất phương trình f(x) > 0nghiệm đúng với mọi x
Vậy không còn mức giá trị nào của m để bất phương trình có nghiệm đúng với mọi x thuộc .
Ví dụ 2: Tìm m để những bất phương trình sau đúng với mọi x thuộc .
a. (m - 3)x2 + (m + 1)x + 2 < 0
b. (m - 1)x2 + (m - 3)x + 4 > 0
Hướng dẫn giải
a. Đặt (m - 3)x2 + (m + 1)x + 2 = f(x)
TH1: m - 3 = 0 ⇔ m = 3. Thay m = 3 vào bất phương trình ta được: 2x + 2 < 0 ⇔ x < -1 (Loại)
TH2: m - 3 ≠ 0 ⇔ m ≠ 3
Để bất phương trình f(x) < 0nghiệm đúng với mọi x
Ta có: mét vuông - 6m + 25 = (m - 3)2 + 16 ≥ 16,∀m
Vậy không còn mức giá trị nào của m để bất phương trình có nghiệm đúng với mọi x thuộc
b. Đặt (m - 1)x2 + (m - 3)x + 4 = f(x)
TH1: m - 1 = 0 ⇔ m = 1. Thay m = 1 vào bất phương trình ta được: -2x + 4 > 0 ⇔ x < 2 (Loại)
TH2: m - 1 ≠ 0 ⇔ m ≠ 1
Để bất phương trình f(x) > 0nghiệm đúng với mọi x
Vậy thì bất phương trình có nghiệm đúng với mọi x thuộc
.
Bài tập tự rèn luyện
Bài 1: Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc : (m - 5)x² - 2x + m + 1 > 0
Bài 2: Tìm m để những bất phương trình sau có nghiệm đúng với mọi x
a.Bài 3: Cho bất phương trình:
Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc .
Bài 4: Tim m để những bất phương trình sau nghiệm đúng với mọi x.
a.
b.
c.
Bài 5: Xác định m để đa thức sau: (3m + 1)x² - (3m + 1)x + m + 4 luôn dương với mọi x.
Bài 6: Tìm m để phương trình: (mét vuông + m + 1)x2 + (2m - 3)x + m - 5 = 0 có 2 nghiệm dương phân biệt
Bài 7: Tìm giá trị tham số để bất phương trình sau nghiệm luôn đúng với mọi x:
a. 5x2 - x + m > 0
b. mx2 - 10x - 5 < 0
c. m(m+2)x2 - 2mx + 2 > 0
d. (m + 1)x2 - 2(m - 1)x + 3m - 3 < 0
Bài 8: Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc R ; (m-5)x² - 2x + m + 1 >0
---------------------------------------------------------------
Mời bạn đọc tham khảo thêm một số trong những tài liệu liên quan đến bài học kinh nghiệm tay nghề:
- Bài tập công thức lượng giác lớp 10Tìm m để bất phương trình có nghiệmBảng công thức lượng giác dùng cho lớp 10 - 11 - 1210 bộ đề thi học kì 1 môn Toán lớp 10
Trên đây là Tìm m để bất phương trình có nghiệm đúng với mọi xVnDoc.com ra mắt tới quý thầy cô và bạn đọc. Chắc hẳn qua nội dung bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức và kỹ năng của bài học kinh nghiệm tay nghề rồi đúng không ạ? Bài viết được tổng hợp gồm có lí thuyết, phương pháp giải và những bài tập tự rèn luyện về tìm m để bất phương tình có nghiệm đúng với mọi x. Hi vọng qua nội dung bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10. Để giúp bạn đọc có thêm nhiều tài liệu học tập hơn thế nữa, VnDoc.com mời bạn đọc cùng tham khảo thêm một số trong những tài liệu học tập những môn được chúng tôi biên soạn và tổng hợp tại những mục sau Tiếng anh lớp 10, Vật lí lớp 10, Ngữ văn lớp 10 ,...
Để giúp bạn đọc hoàn toàn có thể giải đáp được những thắc mắc và trả lời được những thắc mắc khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt thắc mắc tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ tương hỗ trả lời giải đáp thắc mắc của những bạn trong thời gian sớm nhất hoàn toàn có thể nhé.
[embed]https://www.youtube.com/watch?v=RXCPZ9MblhE[/embed]