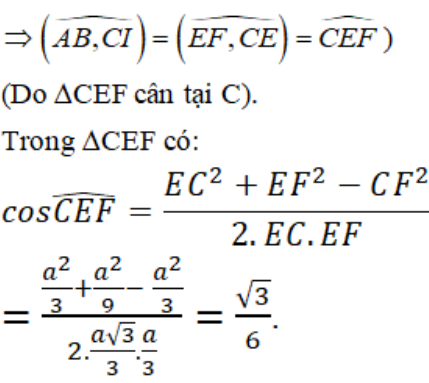Mẹo Hướng dẫn Cho tứ diện đều ABCD cạnh a tính cosin góc giữa hai tuyến đường thẳng AB và CI với I là trung điểm của AD 2022
Bùi Thanh Tùng đang tìm kiếm từ khóa Cho tứ diện đều ABCD cạnh a tính cosin góc giữa hai tuyến đường thẳng AB và CI với I là trung điểm của AD được Update vào lúc : 2022-03-26 16:31:10 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Cho tứ diện đều ABCD cạnh a. Tính...
Câu hỏi: Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai tuyến đường thẳng AB và CI với I là trung điểm của AD
A.32
B.36
C.34
D.12
Đáp án
- Hướng dẫn giải
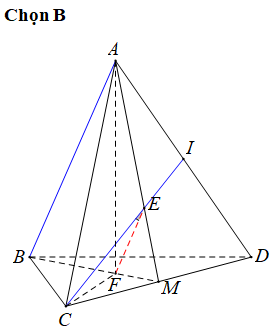
Gọi M là trung điểm của CD
Gọi E và F lần lượt là trọng tâm tam giác ACD và BCD
Ta có:CI=a32;CE =23CI=a33
Tương tự;CF =a33
Xét tam giác AMB có:MEMA=MFMB=13
Suy ra: EF// AB
Câu hỏi trên thuộc đề trắc nghiệm
100 câu trắc nghiệm Vecto trong không khí nâng cao !!Lớp 11 Toán học Lớp 11 - Toán học
Cho tứ diện đều (ABCD) cạnh (a). Tính góc giữa hai tuyến đường thẳng (IC) và (AC), với (I) là trung điểm của (AB).
A.
B.
C.
D.
Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai tuyến đường thẳng AB và CI với I là trung điểm của AD
A. 3 2
B. 3 6
C. 3 4
D. 1 2
Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai tuyến đường thẳng CI và AC, với I là trung điểm của AB?
A. 100
B. 300
C. 1500
D. 1700
Cho tứ diện đều ABCD cạnh AB=1. Gọi M, N, P lần lượt là trung điểm những cạnh AB, BC, AD. Tính khoảng chừng cách giữa hai tuyến đường thẳng CM và NP.
A. 10 10
B. 10 20
C. 3 10 10
D. 3 10 20
Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi α là góc giữa hai tuyến đường thẳng AB và DM, khi đó c o s α cbằng
A . 3 6
B . 2 2
C . 3 2
D . 1 2
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng chừng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Tính khoảng chừng cách giữa AD và BC.
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của những cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai tuyến đường thẳng MG và NP. Khi đó cosα bằng
A. 2 6
B. 2 4
C. 3 6
D. 3 4
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của những cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai tuyến đường thẳng MG và NP. Khi đó cos α bằng
Cho lăng trụ tam giác A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A ' trên mặt phẳng (ABC) là trung điểm O của cạnh AB. Số đo của góc giữa đường thẳng A A ' và mặt phẳng A ' B ' C ' bằng 60 0 . Gọi I là trung điểm của cạnh B ' C ' . Khoảng cách giữa hai tuyến đường thẳng CI và A B ' bằng
A. a 7 7
B. a 5 5
C. a 3 8
D. a 3 2
Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai tuyến đường thẳng AB và CI với I là trung điểm của AD
A. 3 2
B. 3 6
C. 3 4
D. 1 2
Các thắc mắc tương tự
Cho tứ diện đều ABCD cạnh a. Gọi M là trung điểm của C (như hình vẽ). Tính cosin của góc tạo bởi hai tuyến đường thẳng AC và BM.
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng chừng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Tính khoảng chừng cách giữa AD và BC.
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC Khi đó cosin của góc giữa hai tuyến đường thẳng nào sau đây có mức giá trị bằng bằng 3 6 .
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng chừng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (ADH) và DH = a.
Tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng (BCD), AB = 2a. M là trung điểm của AD, gọi φ là góc giữa đường thẳng CM với mp(BCD), khi đó
A. tan φ = 3 2
B. tan φ = 2 3 3
C. tan φ = 3 2 2
D. tan φ = 6 3
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng chừng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).
Cho tứ diện đều ABCD cạnh a. Gọi M là trung điểm của BC. Tính cô-sin của góc giũa hai tuyến đường thẳng AB và DM?
Cho tứ diện đều ABCD, M là trung điểm của BC. Khi đó cosin của góc giữa hai tuyến đường thẳng nào sau đây có mức giá trị bằng 3 6
A. (AB, DM).
B. (AD, DM).
C. (AM, DM).
D. (AB, AM).
[embed]https://www.youtube.com/watch?v=8RSxP3R3yyU[/embed]